N C r の関係があるが小学6年生の算数 場合の数・順列 練習問題プリント ツイート 組み合わせ方、並べ方を、落ちや重なりがないように順序よく整理して、調べる方法を練習できる問題プリントです。 場合の数・順列(1) 答え 場合の数・順列(2) 答え 場合の数順序を区別すれば,項の数は「重複順列」 2 3 =8 通りになる =a 3 3a 2 b3ab 2 b 3 文字の部分が同じものを同類項として整理すれば,文字の組合わせは a 3 , a 2 b , ab 2 ,b 3 で 2 H 3 =4 種類になる ※ これらのうち,順列と組合せには, n P r =r!

クリアー数学a 数a P102 5 組合せ
数a 順列 組み合わせ 問題
数a 順列 組み合わせ 問題- いろいろな組合せの問題 具体的な問題を通して,組合せの考え方に慣れましょう. 例題 男子 $5$ 人女子 $4$ 人から,男子 $2$ 人,女子 $2$ 人の委員を選ぶ方法は何通りあるか. 人は当然区別がつくものと考えます.まず,男子 $5$ 人から $2$ 人を選ぶ方法は,${}_5 \mathrm{C} _2=10$ 通りです.(選ぶ場合の数の問題は大まかに分けると 順列 と 組み合わせ があり,これらは掛け算と割り算を駆使することで求めることができます. では実際に解いてみましょう! 1a,b,cの3人を1列に並べる方法は何通りあるか. *1 解答1 書き出す解き方




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学
定期試験対策 数学a 赤点回避 数学i 公式 場合の数 応用問題 数学A 最大最小 基礎 組み合わせ 順列 確率 ベクトル方程式 漸化式 位置ベクトル 数学b 集合 公式の使い分け ベクトル 円順列 基本 重複順列 ベクトルの基礎 内積 望遠鏡和 まとめ 並び方が指示さ 例えば、上の問題であれば、全部で5つの中から2つを選ぶ場合の組み合わせの数ですので、次のように表現できます。 $$\text{5つの中から2つを選ぶ場合の組み合わせの数}={}_5C_2$$ これを計算すればよいのです。 計算方法は、まず\({}_5C_2\)の\(2\)に注目します。この記事では,「A,B,Cの3文字から全部で7個選ぶ場合の数」のように,同じものがいくつかあってよい「重複組み合わせ」の考え方を説明します. 「重複組合せ」の問題設定としては 選ばれない色のボールがあっても良い場合 選ばれないボールがあっては
場合の数4| 組み合わせのnCrの求め方から性質まで攻略 前々回の記事では,「 n 個のものから r 個選んで並べる場合の数」である順列について説明しました. 「モノを選びとること」を組み合わせといい,「 n 個のものから r 個選ぶ場合の数」を n C r で巡回セールスマン問題もナップサック問題も原理的には列挙すれば 答えが見つかることになっています.しかし 可能な巡回路の数は n! 小学校で扱う場合の数の組み合わせの考え方 順列 (並べ方)とはまた違った数え方をしないといけない組み合わせ。 うまく数えるコツをつかめるととても楽に問題を解くことが出来る単元になります。 今回の記事では、組み合わせの数の数え方について
E 74通り 『少なくとも・・・』ときたら 「問題文と反対の条件の場合の数」を考え、全体の総数から引く。 問題の条件である「男性が少なくとも1人は含まれる」の反対は、「男性が1人も含まれない」言い換えると「女性だけから選ぶ」である。 女性だけこの問題は「 $4$ 桁の整数の数 $$ $4$ 桁の奇数の数」として求めることもできます。遠回りですが、こっちの方が理解しやすいです(場合分けがいらないため)。 問題文からは一見わかりづらいですが、これは重複組み合わせの問題です。 「\(6\) 個のお菓子に、異なる \(3\) 人の名前を重複を許して書く」と考えるとわかりやすいかもしれません。 公式が苦手な人は、モノと仕切りで考えましょう。




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学
例 各位の数が異なる2桁の整数の総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 p 2 =10·9=90 のうち,先頭が0のもの(9個)は1桁になるから,909=81個 (別解) 十の位は0以外の9通り,それぞれ1の位は9通りだから,9×9=81通り さて,この問題を重複組合せの考え方で解いてみましょう. 8 8 個の と, 2 2 本の仕切り を適当に一列に並べると,そのひとつの並び方が上の問題のひとつの整数解の組に対応します. よって,求める整数解の個数は 10C2 = 45 10 C 2 = 45 通りです.つまり4つの異なる1桁の自然数のうち、2つの数の和を出す。 これを6回行ったところ、和は5、6、9、12、13となった。 ただし、重複する計算結果が1つある。 このとき、4つの自然数のうち最大のものとして正しいものはどれか。 ※練習問題のため選択肢なし



教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学



高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
数 学 A 場合の数 例題(9) 練習問題 練習問題+解答 組合せの総数 n C r が整数であることの証明確率 例題(8) 練習問題 練習問題+解答整数の性質 例題(11) 練習問題 練習問題+解答図形の性質 例題(18) 練習問題 練習問題+解答 三角形の角の二等分線この問題を解釈すると、つまり $$ とか $755$ みたいに、「各位の数がどんどん小さくなってく自然数」をすべて数え上げればokです。 さあ、一見するとこの問題は、"順列"のようにも思えSPI練習問題 ② 第3問解答/解説 順列・組み合わせ答え C 順列は特定する必要が無い、つまり不特定のメンバー選定のようなケースでは C を使う、委員長や書記などを選ぶ「特定の人を選別する」パターンでは、 P を使う、としておくと



1




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
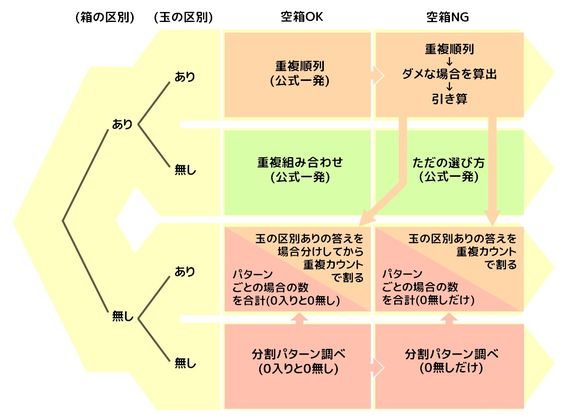
「 ④席の数と要素の数は同じか 」とは、要素をすべて使って並べ替えるのか、 一部だけを使って並べ替える(=席の数が要素の数より少ない)か、ということです。 これらをまとめると、次の表のようになります。 表:席の問題の分類ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。問題文に「選ぶ」という言葉があれば必ず組み合わせ!とは限りません。 問題をよく読んで aとb、bとaそれぞれ入れ替えても同じだ!と考えられるなら組み合わせ。 入れ替えると違うものだ!と考えられるなら順番を数えるときと同じように求めてください!




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学




改訂版 クリアー数学a P115 研究 重複を許して作る組合せ
今回のテーマは重複組み合わせです! 場合の数の中でも難易度が高い重複組合せ はじめに2つ質問です。 質問其の1:重複組合せは得意ですか? 質問其の2:nHrの記号を使わず問題を解いていますか? ・・・ ・・・ 両方ともYESだった人は問題ありません。組合せ数学(くみあわせすうがく、英語 combinatorics )あるいは組合せ論(くみあわせろん)とは、特定の条件を満たす(普通は有限の)対象からなる集まりを研究する数学の分野。 離散数学の中核の一つとされる。特に問題とされることとして、集合に入っている対象を数えたり(数え上げ的通り 可能な商品の組合せは2n 通り. n!




重複組み合わせの問題を解くたった1つの方法とは 公式hは使用注意




高校数学無料問題集 数a 第1章 場合の数と確率 組合せ 桝 ます Note
場合の数が得意な人はここはスキップ。 こちらへどうぞ。 ⇒ 問題11(組み合わせ) ① 4枚のカードから1枚を取り出して、1桁の整数を作ることを考えると、この作り方は4通りある。 ② 4枚のカードから2枚を取り出して、2桁の整数を作ることを考えるとExcelで、複数の値からある合計数に一致する組み合わせを探す。 例えば、「値 100, 78, 25, 66, 1, 」を使って、 合計が1になるような組み合わせは「78, 25, 66, 」となる。 (これはいわゆるナップサック問題の一種) これをExcelに計算してもらう方法。 組分け(グループ分け)問題の解法 (1)区別がつくもの→区別がつくものに組み分けする方法 例題 (11)6人を部屋A、B、Cに分ける場合の数を求めよ。 但し空室があっても良いものとする。 例題 (12)同条件で空室があってはならないとする。 (2)区別が付く




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説




高校数学無料問題集 数a 第1章 場合の数と確率 組合せ 桝 ます Note
高校数学A 場合の数 組分けは単純な問題は教科書レベルの基本問題であるが、実際には「モノが区別できるか否か」「組が区別できるか否か」「組の要素の個数が決まっているか否か」「要素の個数が0個の組があってもよいか」で求め方が変わる SPI における 組み合わせの公式 を用いて確率を求める問題です。 求める場合の数と、すべての場合の数をそれぞれ求め、分数の分子に前者を、分母に後者を当てはめることで確率が求められます。 目次 1 例題1 11 問題1 2 例題2重複のある組み合わせ問題 お店やレストランで決まった数を注文するときのように、組み合わせ結果に同じモノがある組み合わせです。 これは本来順序を問わない組み合わせの問題なのですが、「仕切り板」を考えることで「 同じモノが含まれるときの



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




高校数学 数a 勉強動画 組合せ 重複編の問題 19ch
数学A場合の数の解き方:硬貨の問題その1 それでは、問題を解きながら見ていきましょう。 問題 次の硬貨を全部または一部を使ってちょうど支払できることができる金額は何通りあるか? 1)10円硬貨5枚、100円硬貨3枚、500円硬貨2枚。 硬貨の問題の場合




高校数学 数a 勉強動画 組み合わせ 基本編の問題 19ch



1




高校数学 数a 17 組合せ 道順編 Youtube




順列pと組み合わせcの違いと 簡単 な見分け方



小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




組み合わせをわかりやすく解説 10人を4 2 2 2人の4組に分ける 高校数学




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




高校数学 数a 勉強動画 組合せ 道順編の問題 19ch




組分け問題全8パターン Aを解説 区別の有無で数学的な考え方が変わる 遊ぶ数学




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




数aの重複を許して作る組み合わせの範囲です ここに書いてある解説だけでは分からなかっ Clear




高校数学 数a 7 順列 基本編 Youtube




数aの順列と組み合わせの問題です 誰か教えてください 急いでます Clear



2



48s96ub7b0z5f Net Saitankeiro



組み分け 部屋分け 問題全8パターンと解き方 数a 場合の数確率 そうちゃ S 図解英数ゼミナール
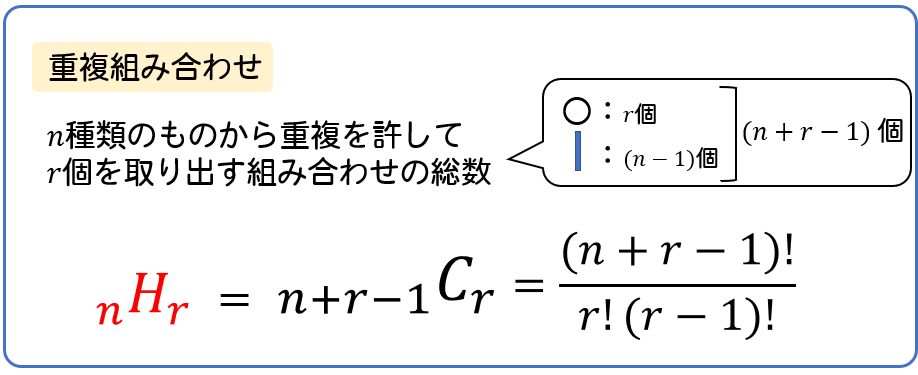



重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ




高1の数aの組み合わせあたりの問題です 6 です ちなみに答えは1でした Clear




3講 順列 1章 場合の数と確率 問題集 高校数学a
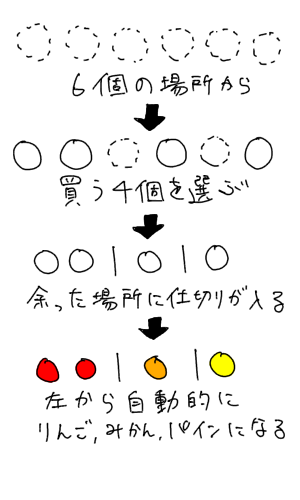



重複組み合わせは絵を描けば理解できる イラストで解説 理数白書



数aで組み合わせの問題50c47の答えを教えて下さい 50c4 Yahoo 知恵袋



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b
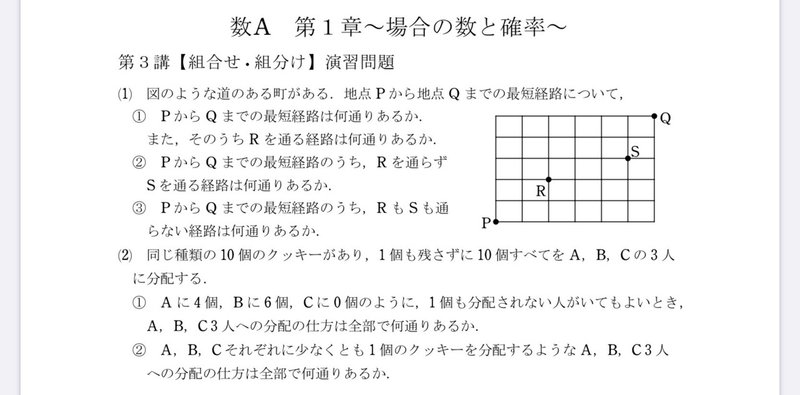



高校数学無料問題集 数a 第1章 場合の数と確率 組合せ 桝 ます Note



同じものを含む順列の問題 京極一樹の数学塾




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん



数a組み合わせ 点字の問題なんですが 点字は縦3列 横2列の6つの場 Yahoo 知恵袋




高校数学a 場合の数 組合せ頻出 男女を選ぶ問題 高校生 数学のノート Clear



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




高校 数学a 場合の数31 pとcの違い 11分 Youtube




高校数学 数a 18 組合せ 重複編 Youtube



数a順列組み合わせ 2番と3番の問題について なぜ分数になる Yahoo 知恵袋




順列と組み合わせの公式とその違い 問題付き 理系ラボ




数a 教えてください この問題の解き方が分かりません Clear




組分け問題全パターン おいしい数学




高校数学 数a 勉強動画 組合せ 文字編の問題 19ch




高校数学 確率 玉が登場する確率問題の解き方 数学の面白いこと 役に立つことをまとめたサイト




高校数学無料問題集 数a 第1章 場合の数と確率 組合せ 桝 ます Note




クリアー数学a 数a P102 5 組合せ




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




高校数学 数a 9 組合せと図形の問題 Youtube




高1 数a 場合の数 4 組合せ 高校生 数学のノート Clear



重複組合せ




18 センター数学 a 集合を楽に解く 怜悧玲瓏 高校数学を天空から俯瞰する




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学



組み合わせ C とは 公式や計算方法 は何通り 受験辞典



数a組み合わせ最短経路 よくある基盤の目状の道路が等間隔にある の順列を Yahoo 知恵袋




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




数学a 重複組み合わせ問題 場合の数 チャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru
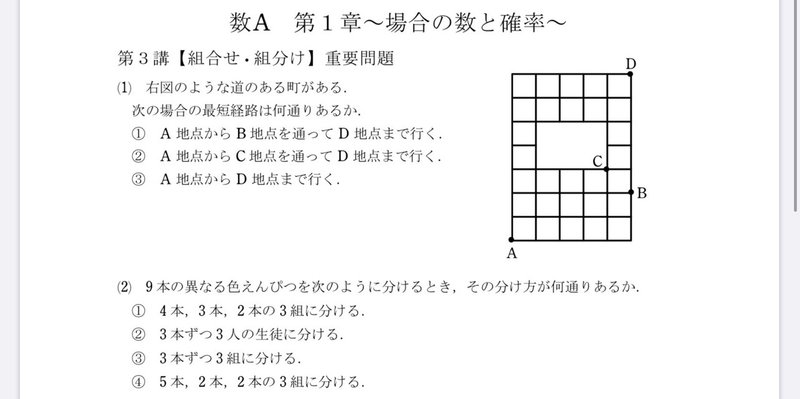



高校数学無料問題集 数a 第1章 場合の数と確率 組合せ 桝 ます Note




高校数学a 重複組合せ Nhr 受験の月
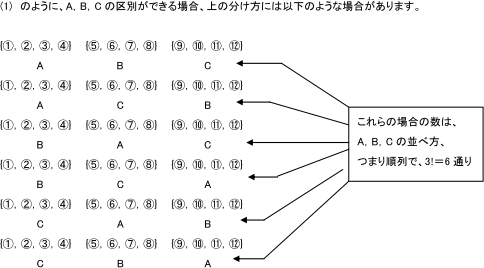



区別がない組分け 数学 苦手解決q A 進研ゼミ高校講座




高校数学a 同じものを含む順列 N P Q R 受験の月




組み合わせ C とは 公式や計算方法 は何通り 受験辞典




数学a 場合の数勉強法 答え合わない 時間かかる を解決する 場合の数勉強法



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




高校数学a 組合せの計算1 Ncr 例題編 映像授業のtry It トライイット




高校数学 数a 勉強動画 順列 基本編の問題 19ch




5講 組合わせ 1章 場合の数と確率 問題集 高校数学a




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学a 組合せ の確率2 応用 練習編 映像授業のtry It トライイット




高校数学 数a 14 組み合わせ 基本編 Youtube
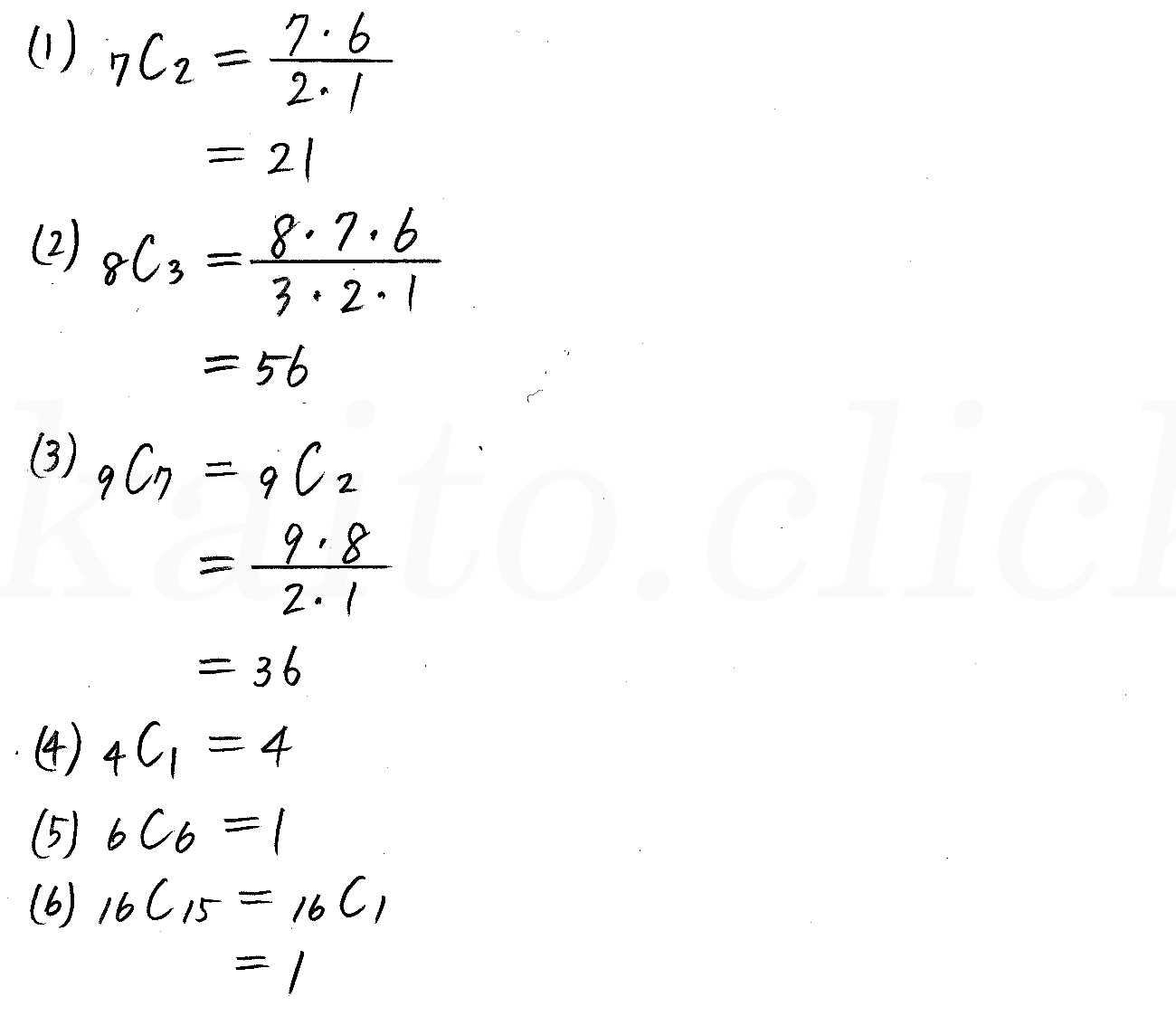



改訂版 4プロセス数学a P116 4 組合せ



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




原田 浩明 Sサクシード223 組に分ける問題 同じものを含む順列 高校 数学 数a 組合せ




高校数学無料問題集 数a 第1章 場合の数と確率 組合せ 桝 ます Note




高校数学a Npr と Ncr の使い分け 練習編 映像授業のtry It トライイット
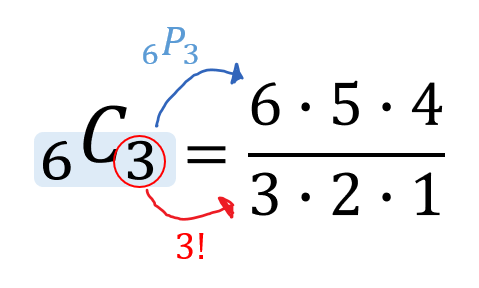



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ
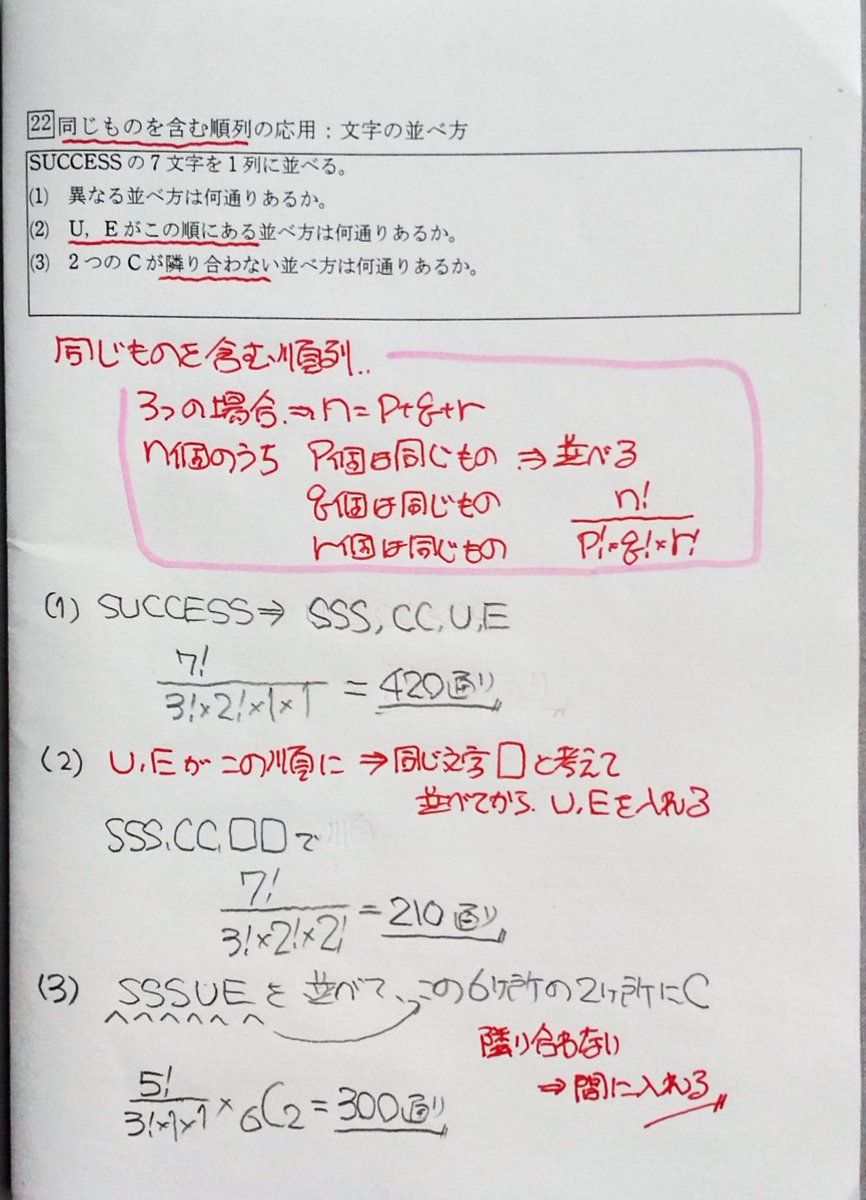



原田 浩明 Sサクシード223 組に分ける問題 同じものを含む順列 高校 数学 数a 組合せ




高校数学a 組分け問題全パターン 受験の月




高校数学a 場合の数 組合せ頻出 男女を選ぶ問題 高校生 数学のノート Clear




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学
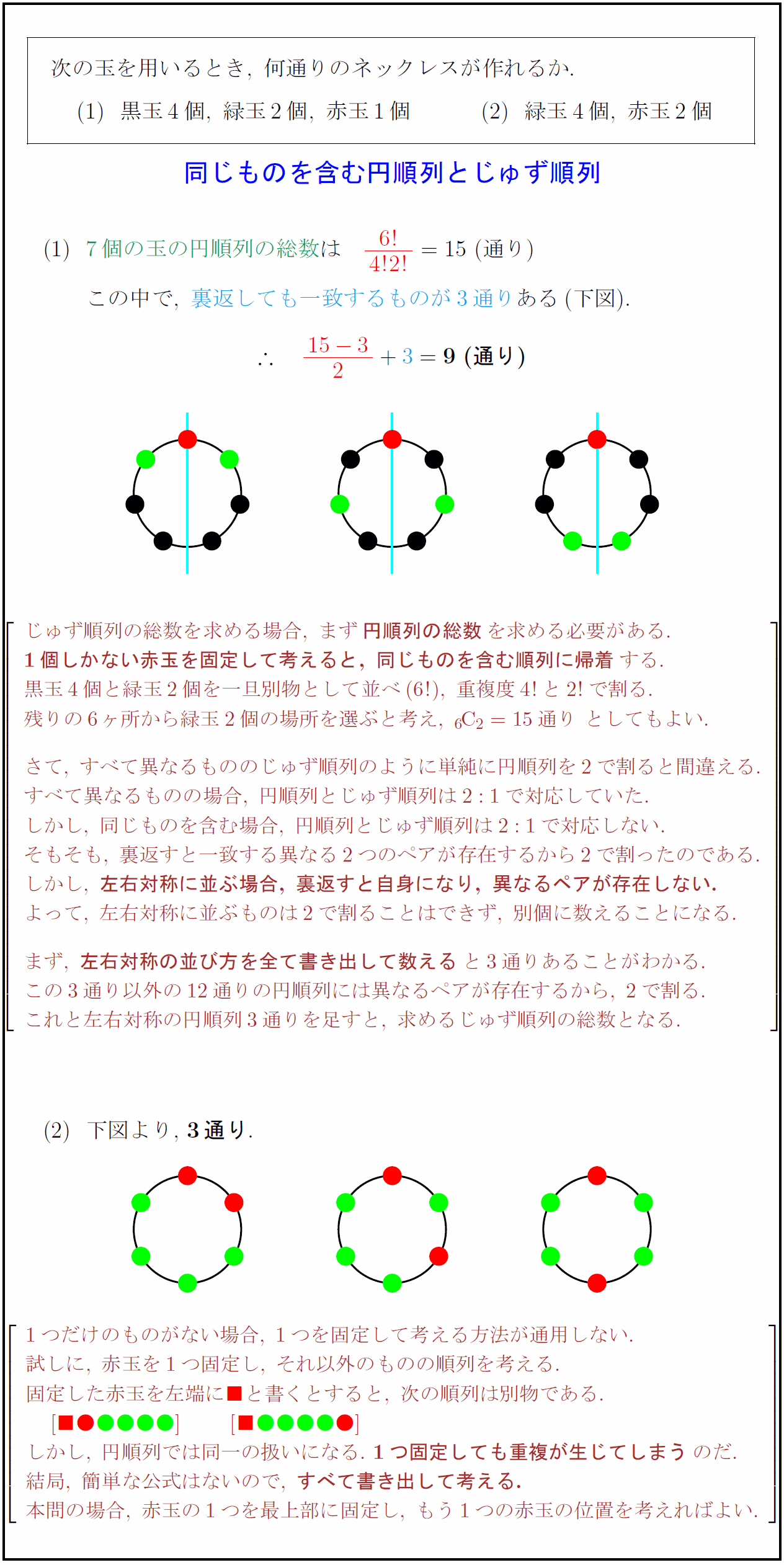



高校数学a 同じものを含む円順列とじゅず順列 受験の月



1




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



数学i Aチェック リピート 第7章 2順列 組合せ 10 最短経路 Pukiwiki



1




5講 組合わせ 1章 場合の数と確率 問題集 高校数学a




重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ




高校数学 数a 勉強動画 組合せ 男女編の問題 19ch




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




高校数学a 一定の順序を含む順列 受験の月




3講 順列 1章 場合の数と確率 問題集 高校数学a




高校数学無料問題集 数a 第1章 場合の数と確率 組合せ 桝 ます Note




高校数学 組み合わせ コンビネーション Ncr の計算方法のコツ できるだけ楽に計算しよう 数学の面白いこと 役に立つことをまとめたサイト




5講 組合わせ 1章 場合の数と確率 問題集 高校数学a



0 件のコメント:
コメントを投稿