第46問 正八角形 図形ドリル 6年生 台形 正八角形 面積比 ★★★★★☆(算オリ・灘中受験生レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げてい正八 角形。 楽天市場サイズ別 > ミラー(正八角形タイプ):鏡 インテリアミラー工房 jha 「stop(止まれ)」を表すには、赤い八角形を採用している国・地域が比較的多い。 根号の入れ子状態のものは、やはり折れるのか、 次回は正五角形を折ってみ偏平化した六角形又は八角形断面とは、正六角形断面又は正八角形断面を横幅をそのままで縦方向に拡大、偏平化した形状である。 例文帳に追加 The flattened hexagonal or octagonal cross section is a shape flattened by vertically expanding a regularly hexagonal or octagonal cross section
怎么在纸上画出正八边形 百度经验
正八角形 面积 小学生
正八角形 面积 小学生-使用目的 Φ600の内接する正八角形の1辺の長さを求めたかった ご意見・ご感想 円の半径r=300でのn=8の多角形の1辺の長さaはではなくて?円 鏡 正八角形 正八角 正八角鏡 100% 国産 日本製 鏡 壁掛け ミラー 壁掛け 八角 八角形 オクタゴン 北欧 シンプル ウオールミラー 姿見 鏡 全身 おしゃれ 軽量 鏡 正八角形 500x500mm シンプルカット 日本製 鏡 壁掛け ミラー 壁掛け 5mm厚 取付金具と説明書 壁掛け鏡 壁に直付け ウオールミラー




3种方法来得到一个正八边形
正多面体は、正四面体、正六面体、正八面体、正12面体、正面体の5種類しかない。 正四面体と立方体は簡単にできる。 これをもとに、他の立体を作図してみよう。 まずネットでそれぞれの多面体を調べてみよう。 どう作図できるか浮かんでくる。 1辺が180cmの正方形から、正八角形を作りたいです。 正八角形の1辺は何cmになりますか?求め方の式もしりたいです、、! 1つは計算で出す方法。1つは折り目を使って正八角形を作る方法(こちらは余談です)。 計算で正八角形の一辺や、正方形から切り取るべき長さを計算する方法第47問 正方形と正八角形 図形ドリル 6年生 正八角形 正方形 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。 図形ドリルでは,色々なタイプの図形問題を取り上げ
前回ゼンタングルで正八角形を書くのにちょっと苦労したので、忘れないうちに正八角形の書き方をまとめておきます。 小学校か中学校の算数?数学?の問題でもありましたね〜(^^;) wwwmgraffiticom 正八角形の書き方 まずは正方形を書きます 次に対角線を書きます 対角線の交点と四角形の頂点 正n角形の1つの内角は、 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180×(52)/5 = 108° になるねOの正八面体はaとbの2つと稜共有・defgの4つと頂点共有・ の頂点において他の4つの正八面体と頂点共有している for octahedron "O"
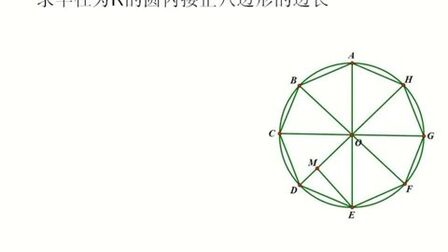
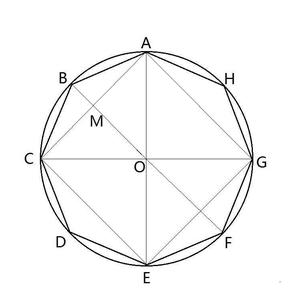
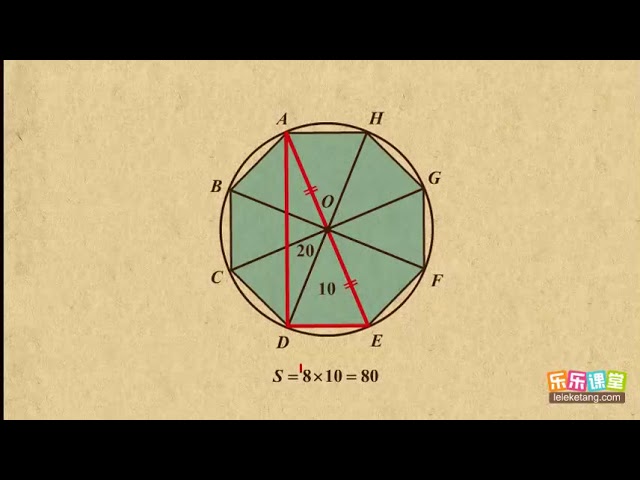
正三角形なのでそれぞれの角は60 です。 そこで円の中心から正三角形の頂点へ線をひきます。 そうすると2辺が10の三角形が3つできます。 三八角形の内角の和は1080度である。 項目を8本の放射線に分けて、8つの項目の大小を対比する図表を、「オクタゴンチャート 要曖昧さ回避 」という。;左図のように、半径Rの円Oがあり、 その中に内接する正8角形の面積を考えました。 見通し 正8角形ですから、図の AOBと合同な二等辺三角形が8個あります。




5年算数 正多角形と円 正八角形をかこう Youtube



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫
上のような2パターンの 正八角形の面積を求める方法 について解説していきます。 この問題を解くためには中学3年生で学習する「三平方の定理」の知識が必要となります。正四面体 正三角形 4 6 4 立方体 正方形 8 12 6 正八面体 正三角形 6 12 8 正十二面体 正五角形 30 12 正二十面体 正三角形 12 30 双対}双対}双対 愛知教育大学 小谷健司 asc 数学b 第4 回立方体と正八面体の展開図の双対正八 角形 面積。 八角形 (斜線部分の面積を求める問題です) また、新しいところでは昨年度の灘中(1日目9番)で という問題が出題されました。




正八边形怎样剪更简单 百度经验




怎么在纸上画出正八边形 Iiiff互动问答平台
正八面体 正三角形 4 6 12 正十二面体 正五角形 3 30 正二十面体 正三角形 5 12 30 体積比と表面積比 編集 相似比が 四谷大塚 予習シリーズ のテキストは四谷大塚よりお買い求め下さい。 著作権は中学受験の算数・理科ヘクトパスカルに帰属します。正n角形の頂点の個数sは,面が正m角形であるとき,頂点数はmn個できるが,1頂点の周りの面rの数だけ重なるから, s=mn×1/r なる関係が成り立つ.これから rs=mn すなわち,(*)は, (正多角形の辺の個数)×(正多面体の面の個数) に等しい.よって正八角形a1a2 a8 の4 個の頂点を結んでできる四角形のうち,与えられた条件( ) を満たすものは,辺の1 つ,または対角線の1 つが正八角形a1a2 a8 の外接円の 直径となる場合である. 線分a1a5 を辺または対角線にもつ四角形の個数は,残り2 つの頂点の選び方を



コンパスと定規を使った正八角形の描き方 図形の描き方014a 夏貸文庫




八边形 维基百科 自由的百科全书
正多面体の頂点の数 つづいて正多面体の頂点の数です。 結論から言うと以下の公式で求められます。 (頂点の数)=(面の頂点の数)×(面の数)÷(1点に集まる面の数) たとえば正四面体について考えてみましょう。 面の形は正三角形なので「面の厚み15X縦100X横0㎜ 材質:アガチス P8 長方形 厚み15X縦100X横300㎜ 材質:アガチス P9 正方形 厚み15X縦150X横150㎜ 多角形の外角の和は360° なので,1つの外角の大きさは, 正六角形 正八角形 正十角形 が360°÷10=36°, 正十二角形 が360°÷12=30° と求まります。 よって,1つの内角の大きさは, 正六角形 が180°-60°=1°, 正八角形 が180°-45°=135°, 正十角形 が180°-36°=144




古建大成 没有数学基础的古代木匠 设计的八角亭居然涉及无理数 每日头条



八角形正八角形图标免费下载 图标lybqoglp icon图标网



多边形正八边形简笔画 多边形正八边形简笔画画法




3种方法来得到一个正八边形




正八边形的简便计算公式是什么 给定正八边形的面积




11 029 Best Octagonal Images Stock Photos Vectors Adobe Stock



答疑 请问正八边形怎样画 如何用cad画八边形 羽兔网问答



1




正八边形怎么制作 百度经验




八边形 维基百科 自由的百科全书




八边形的体积公式 数学 21




3种方法来得到一个正八边形



正八边形 快懂百科




正多边形几何学七角正八角形连接png图片素材免费下载 图片编号 Png素材网



几何 正八边形的探索 二 原创 以题会友 微信公众号文章阅读 Wemp



求直径160圆形的内切正八边形边长 信息阅读欣赏 信息村 K0w0m Com




8边形有几条对称轴图解 百度经验




八角形 Wikipedia



正八边形画法 万图壁纸网




怎么在纸上画出正八边形 百度经验
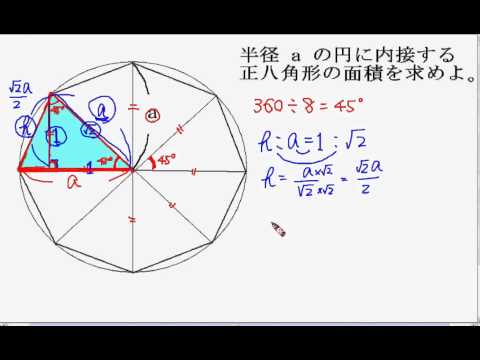



中3数学 正八角形の面積 Youtube




八角形面積計算八角形面積公式 百度知道狀態 Ekcup



几何剖分 从正八边形到正方形 五边形



如何用cad画正八边形 3d溜溜网



几何 正八边形的探索 二 原创 以题会友 微信公众号文章阅读 Wemp



等边八角形怎么画 万图壁纸网



小学奥数之正八边形 留言



70以上8 角形角度 シモネタ



1




八边形对角线计算公式 正八边形边长计算 三人行教育网 Www 3rxing Org




2 804 Background Octagonal Design Wall Murals Canvas Prints Stickers Wallsheaven



正八边形 西瓜视频搜索



正八边形第1页 驾考预约大全



正八边形分割 万图壁纸网




3种方法来得到一个正八边形



如何得到一个正八边形 生活小百科
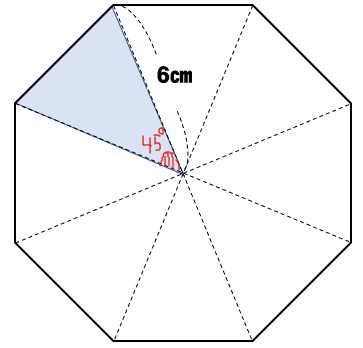



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ




正多边形 属性




八边形 维基百科 自由的百科全书
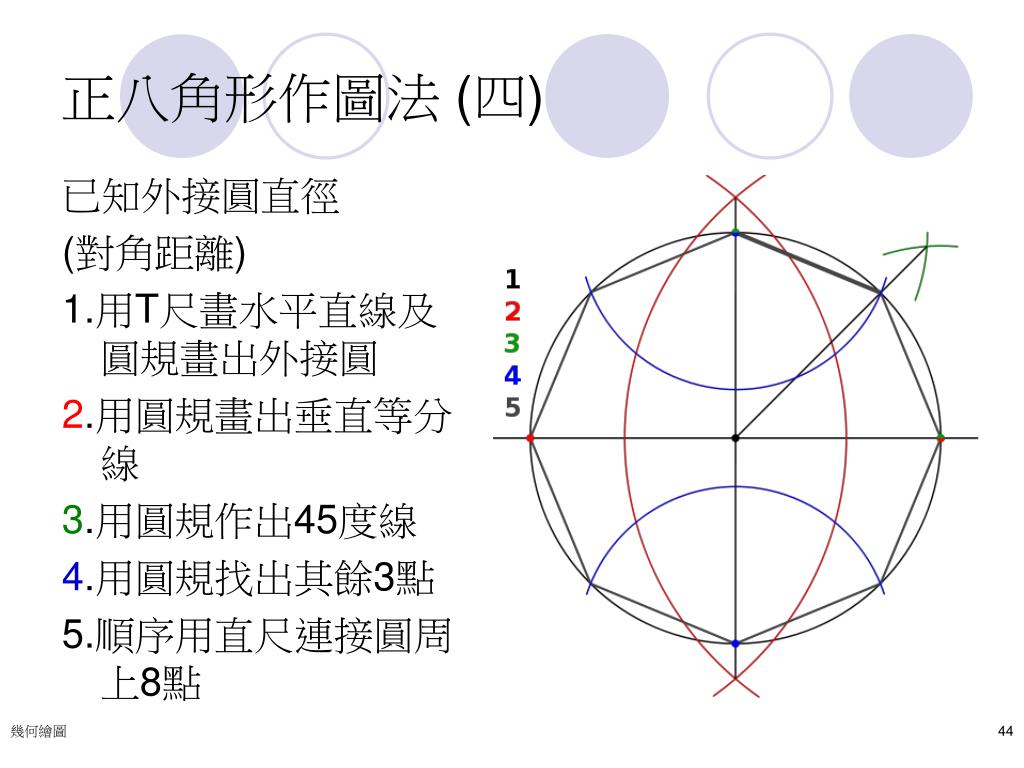



Ppt 幾何繪圖g Eometrical Drawing Powerpoint Presentation Free Download Id




八边形 维基百科 自由的百科全书




怎么在纸上画出正八边形 Iiiff互动问答平台



一辺1の正八角形の対角線の長さを教えてください Aeの長さの出し方を教えてく Yahoo 知恵袋



正八角形 Geogebra




正八边形 360百科
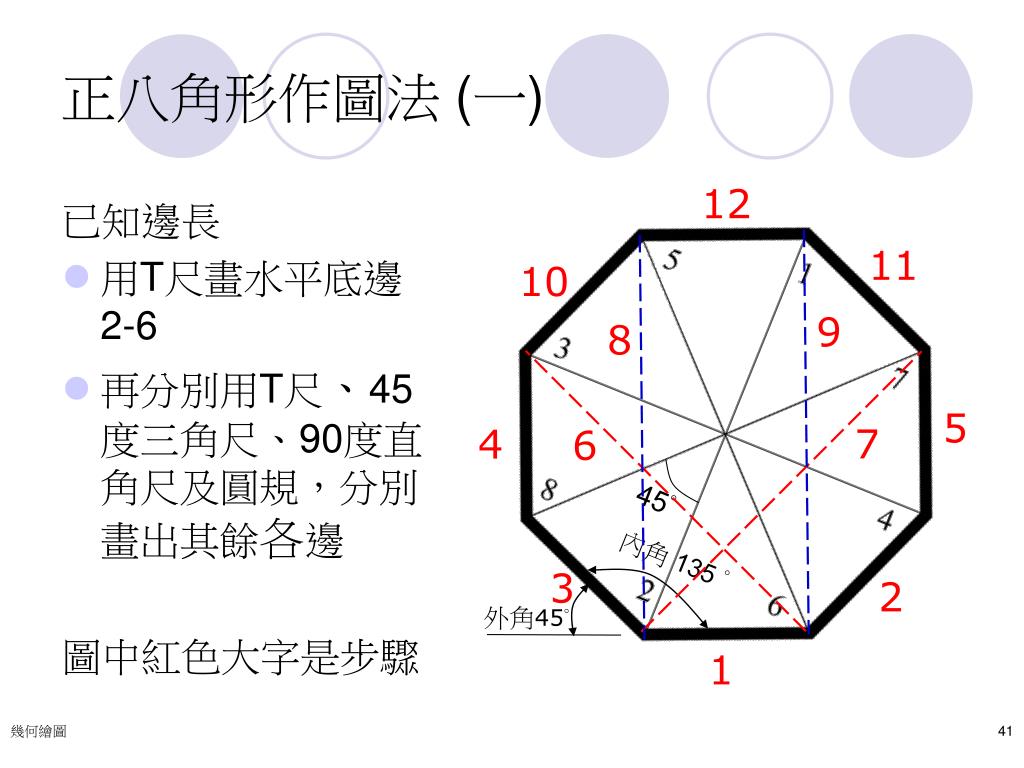



Ppt 幾何繪圖g Eometrical Drawing Powerpoint Presentation Free Download Id



正八角形 Geogebra




八边形对角线计算公式 正八边形边长计算 三人行教育网 Www 3rxing Org




八角形怎么画 八角形正确的画法 无师自通网



正八角形の折り方a 折り紙 Asoppa レシピ あそっぱ
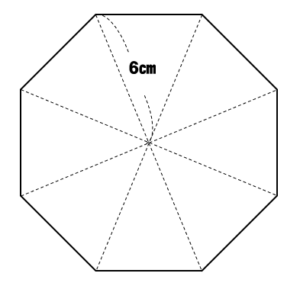



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ



如何用几何画板自定义工具画正八边形




八角形 Wikipedia




3种方法来得到一个正八边形



1




3种方法来得到一个正八边形




多边形正八边形简笔画 多边形正八边形简笔画画法




正八角形的内角 八角形的内角是多少度 三人行教育网 Www 3rxing Org



正八边形画法 万图壁纸网




正八邊形中的等積變換 含原面積 Youtube



求直径160圆形的内切正八边形边长 信息阅读欣赏 信息村 K0w0m Com




正八边形 邱福星的教学页面



Hqrtsmvnxhjqvm



Python Turtle画正八边形 百度经验



1




正八角形の作図 正方形から正八角形の作図の仕方を教えてください 数学 教えて Goo



正八邊形外接圓 Geogebra



多边形正八边形简笔画 多边形正八边形简笔画画法
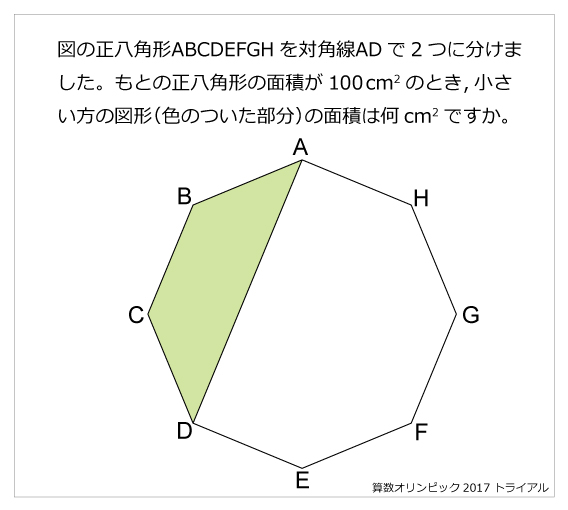



正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦



圆内接正八边形画法 搜狗搜索




正八边形计算器




八边形 维基百科 自由的百科全书



求直径160圆形的内切正八边形边长 信息阅读欣赏 信息村 K0w0m Com



正八边形 西瓜视频搜索



正八边形怎么画 万图壁纸网



70以上8 角形角度 シモネタ




正八边形的画法步骤图 搜狗图片搜索




八邊形 Wikiwand




电路行为 4 5级挑战在线练习问题 Brilliant Vwin登录器



Mhkoffbjwymazm



九年级数学 正六边形和正八变形的内心 怎么求lmn的面积 好题 网易公开课




422 Best 八角形 Images Stock Photos Vectors Adobe Stock




八边形 维基百科 自由的百科全书




正八角形の性質について 添付画像の図 正八角形について Ahiが直 数学 教えて Goo




八角形畫法sketchup Uhlwc



02正八边形的相关计算圆2 初中数学初三 Youtube



画八角形公式 西瓜视频



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋



一种正八边形碳纤维管复合方钢管混凝土承压构件的制作方法



求问如何建立八边形电感的3d模型 因为它不是正八边形 每圈都会多一点 Hfss使用问答



请问是正八边形吗




正八边形图片大全 正八边形设计素材 正八边形模板下载 正八边形图库 昵图网soso Nipic Com
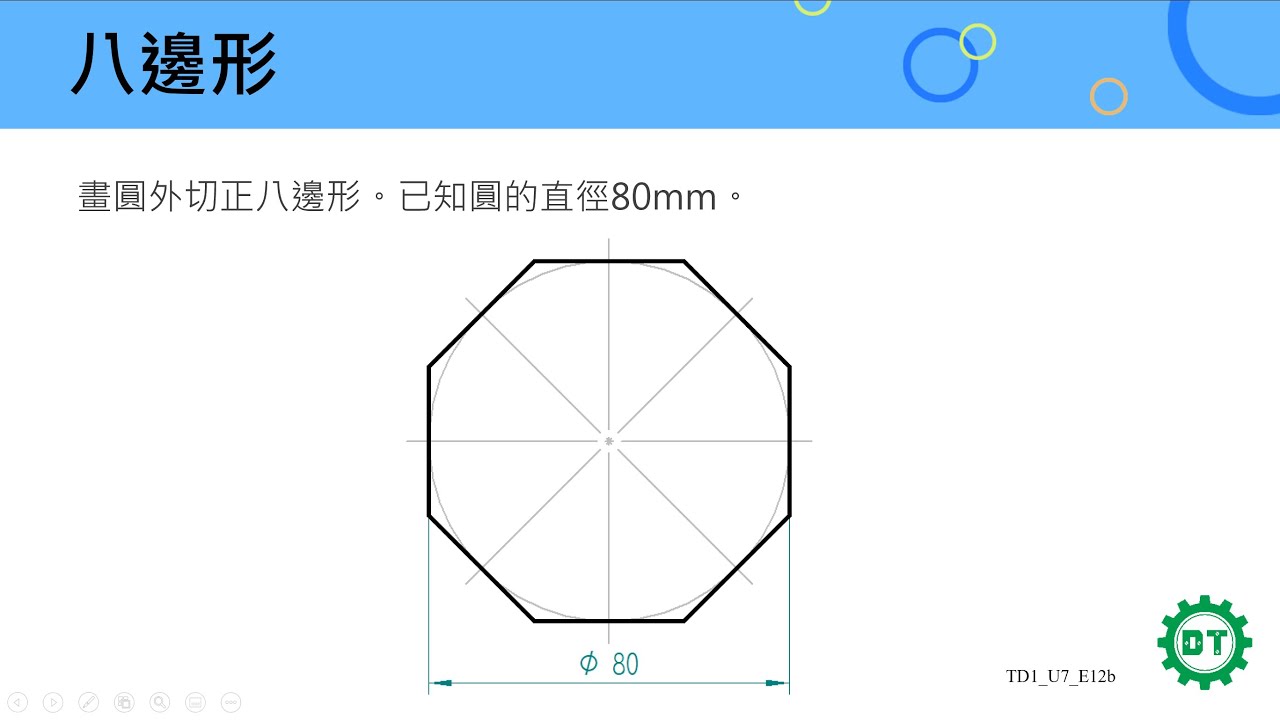



工程繪圖 八邊形 正八邊形3 Youtube
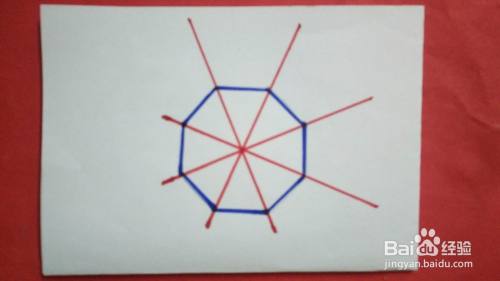



8边形有几条对称轴图解 百度经验



正八边形分割 万图壁纸网
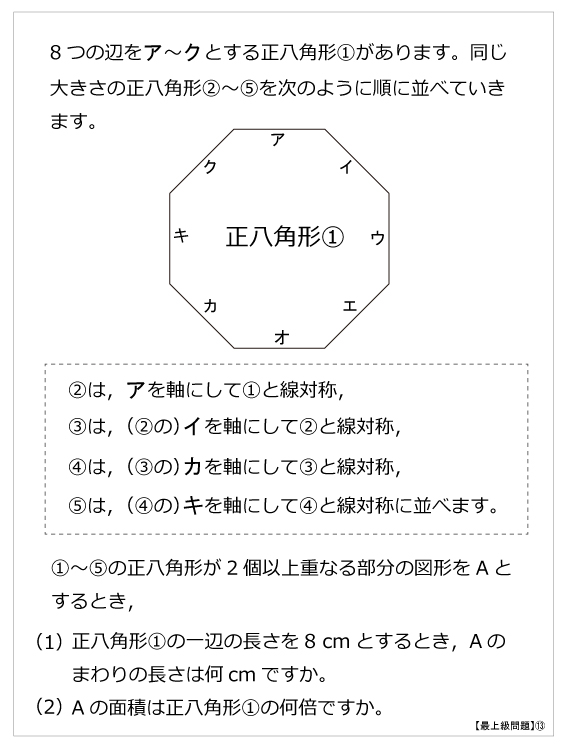



正八角形 算数星人のweb問題集 中学受験算数の問題に挑戦




忘れないうちに正八角形の書き方まとめ M S Graffiti ミミの楽描き帖




3种方法来得到一个正八边形



0 件のコメント:
コメントを投稿